



Visualizing Collinearity Diagnostics
Version 0.1.2
The VisCollin package provides methods to calculate
diagnostics for multicollinearity among predictors in a linear or
generalized linear model. It also provides methods to visualize those
diagnostics following Friendly & Kwan (2009), “Where’s Waldo:
Visualizing Collinearity Diagnostics”, The American
Statistician, 63, 56–65.
These include:
| CRAN version | install.packages("VisCollin") |
| Development version | remotes::install_github("friendly/VisCollin") |
library(VisCollin)
library(dplyr)
library(tidyr)
library(car)
library(corrplot)This example uses the cars data set containing various
measures of size and performance on 406 models of automobiles from 1982.
Interest is focused on predicting gas mileage, mpg.
data(cars)
str(cars)
#> 'data.frame': 406 obs. of 10 variables:
#> $ make : Factor w/ 30 levels "amc","audi","bmw",..: 6 4 22 1 12 12 6 22 23 1 ...
#> $ model : chr "chevelle" "skylark" "satellite" "rebel" ...
#> $ mpg : num 18 15 18 16 17 15 14 14 14 15 ...
#> $ cylinder: int 8 8 8 8 8 8 8 8 8 8 ...
#> $ engine : num 307 350 318 304 302 429 454 440 455 390 ...
#> $ horse : int 130 165 150 150 140 198 220 215 225 190 ...
#> $ weight : int 3504 3693 3436 3433 3449 4341 4354 4312 4425 3850 ...
#> $ accel : num 12 11.5 11 12 10.5 10 9 8.5 10 8.5 ...
#> $ year : int 70 70 70 70 70 70 70 70 70 70 ...
#> $ origin : Factor w/ 3 levels "Amer","Eur","Japan": 1 1 1 1 1 1 1 1 1 1 ...Fit a model predicting gas mileage (mpg) from the number
of cylinders, engine displacement, horsepower, weight, time to
accelerate from 0 – 60 mph and model year (1970–1982). Perhaps
surprisingly, only weight and year appear to
significantly predict gas mileage. What’s going on here?
cars.mod <- lm (mpg ~ cylinder + engine + horse + weight + accel + year,
data=cars)
Anova(cars.mod)
#> Anova Table (Type II tests)
#>
#> Response: mpg
#> Sum Sq Df F value Pr(>F)
#> cylinder 12 1 0.99 0.32
#> engine 13 1 1.09 0.30
#> horse 0 1 0.00 0.98
#> weight 1214 1 102.84 <2e-16 ***
#> accel 8 1 0.70 0.40
#> year 2419 1 204.99 <2e-16 ***
#> Residuals 4543 385
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1lmtest::coeftest() shows the coefficients, \(\hat{\beta_j}\), their standard errors
\(s(\hat{\beta_j})\) and associated
\(t\) statistics, \(t = \hat{\beta_j} / s(\hat{\beta_j})\). As
we will see, the standard errors of the non-significant predictors have
been inflated due to high multiple correlations among the predictors,
making the \(t\) statistics
smaller.
lmtest::coeftest(cars.mod)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.45e+01 4.76e+00 -3.05 0.0024 **
#> cylinder -3.30e-01 3.32e-01 -0.99 0.3212
#> engine 7.68e-03 7.36e-03 1.04 0.2973
#> horse -3.91e-04 1.38e-02 -0.03 0.9775
#> weight -6.79e-03 6.70e-04 -10.14 <2e-16 ***
#> accel 8.53e-02 1.02e-01 0.84 0.4038
#> year 7.53e-01 5.26e-02 14.32 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1It is often recommended to examine the correlation matrix of the predictors to diagnose collinearity problems. In the general case, this advice is misguided, because it is not the 0-order correlations that matter, but rather the multiple correlations predicting each independent variable from the others, \(R_{x_j | \text{others}}\).
Nonetheless, it is instructive to examine the correlations.
R <- cars |>
select(cylinder:year) |>
tidyr::drop_na() |>
cor()
100 * R |> round(digits = 2)
#> cylinder engine horse weight accel year
#> cylinder 100 95 84 90 -52 -36
#> engine 95 100 90 93 -56 -38
#> horse 84 90 100 87 -70 -42
#> weight 90 93 87 100 -43 -32
#> accel -52 -56 -70 -43 100 30
#> year -36 -38 -42 -32 30 100Or, better yet, use corrplot::corrplot.mixed() to
visualize them, using color and shading of glyphs,
corrplot.mixed(R, lower = "square", upper = "ellipse", tl.col = "black")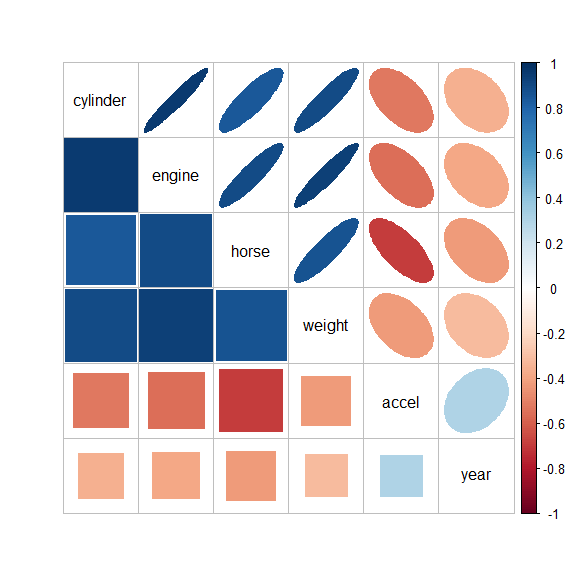
The message here seems to be that there are two clusters of
predictors with high correlations: {cylinder,
engine, horse and weight}, and
{accel, year}.
Variance inflation factors measure the effect of multicollinearity on the standard errors of the estimated coefficients and are proportional to \(1 / (1 - R^2_{x_j | \text{others}})\).
We check the variance inflation factors, using
car::vif(). We see that most predictors have very high
VIFs, indicating moderately severe multicollinearity.
vif(cars.mod)
#> cylinder engine horse weight accel year
#> 10.63 19.64 9.40 10.73 2.63 1.24
sqrt(vif(cars.mod))
#> cylinder engine horse weight accel year
#> 3.26 4.43 3.07 3.28 1.62 1.12According to \(\sqrt{\text{VIF}}\),
the standard error of cylinder has been multiplied by 3.26
and it’s \(t\)-value divided by this
number, compared with the case when all predictors are uncorrelated.
engine, horse and weight suffer a
similar fate.
The diagnostic measures introduced by Belsley (1991) are based on the eigenvalues \(\lambda_1, \lambda_2, \dots \lambda_p\) of the correlation matrix \(R_{X}\) of the predictors (preferably centered and scaled, and not including the constant term for the intercept), and the corresponding eigenvectors in the columns of \(\mathbf{V}_{p \times p}\).
colldiag() calculates:
Condition indices: The smallest of the eigenvalues, those for which \(\lambda_j \approx 0\), indicate collinearity and the number of small values indicates the number of near collinear relations. Because the sum of the eigenvalues, \(\Sigma \lambda_i = p\) increases with the number of predictors \(p\), it is useful to scale them all in relation to the largest. This leads to condition indices, defined as \(\kappa_j = \sqrt{ \lambda_1 / \lambda_j}\). These have the property that the resulting numbers have common interpretations regardless of the number of predictors.
For completely uncorrelated predictors, all \(\kappa_j = 1\).
\(\kappa_j \rightarrow \infty\) as any \(\lambda_k \rightarrow 0\).
In terms of the eigen-decomposition, variance inflation factors can be expressed as \[ \text{VIF}_j = \sum_{k=1}^{p} \frac{V^2_{jk}}{\lambda_k} \; . \]
Variance decomposition proportions: Large VIFs indicate variables that are involved in some nearly collinear relations, but they don’t indicate which other variable(s) each is involved with. For this purpose, Belsley et. al. (1980) and Belsley (1991) proposed calculation of the proportions of variance of each variable associated with each principal component as a decomposition of the coefficient variance for each dimension.
For the current model, the usual display contains both the condition indices and variance proportions. However, even for a small example, it is often difficult to know what numbers to pay attention to.
(cd <- colldiag(cars.mod, center=TRUE))
#> Condition
#> Index Variance Decomposition Proportions
#> cylinder engine horse weight accel year
#> 1 1.000 0.005 0.003 0.005 0.004 0.009 0.010
#> 2 2.252 0.004 0.002 0.000 0.007 0.022 0.787
#> 3 2.515 0.004 0.001 0.002 0.010 0.423 0.142
#> 4 5.660 0.309 0.014 0.306 0.087 0.063 0.005
#> 5 8.342 0.115 0.000 0.654 0.715 0.469 0.052
#> 6 10.818 0.563 0.981 0.032 0.176 0.013 0.004Belsley (1991) recommends that the sources of collinearity be
diagnosed (a) only for those components with large \(\kappa_j\), and (b) for those components
for which the variance proportion is large (say, \(\ge 0.5\)) on two or more
predictors. The print method for "colldiag" objects has a
fuzz argument controlling this.
print(cd, fuzz = 0.5)
#> Condition
#> Index Variance Decomposition Proportions
#> cylinder engine horse weight accel year
#> 1 1.000 . . . . . .
#> 2 2.252 . . . . . 0.787
#> 3 2.515 . . . . . .
#> 4 5.660 . . . . . .
#> 5 8.342 . . 0.654 0.715 . .
#> 6 10.818 0.563 0.981 . . . .The mystery is solved: There are two nearly collinear relations among the predictors, corresponding to the two smallest dimensions.
Note that the high variance proportion for year (0.787)
on the second component creates no problem and should be ignored because
(a) the condition index is low and (b) it shares nothing with other
predictors.
The simplified tabular display above can be improved to make the patterns of collinearity more visually apparent and to signify warnings directly to the eyes. A “tableplot” (Kwan et-al., 2009) is a semi-graphic display that presents numerical information in a table using shapes proportional to the value in a cell and other visual attributes (shape type, color fill, and so forth) to encode other information.
For collinearity diagnostics, these show:
cond.max).The tableplot below encodes all the information from the values of
colldiag() printed above (but using prop.col
color breaks such that variance proportions < 0.3 are shaded white).
The visual message is that one should attend to collinearities with
large condition indices and large variance proportions
implicating two or more predictors.
tableplot(cd, title = "Tableplot of cars data", cond.max = 30 )
The standard biplot (Gabriel, 1971; Gower& Hand 1996) can be regarded as a multivariate analog of a scatterplot, obtained by projecting a multivariate sample into a low-dimensional space (typically of 2 or 3 dimensions) accounting for the greatest variance in the data. With the symmetric (PCA) scaling used here, this is equivalent to a plot of principal component scores of the mean-centered matrix \(\widetilde{\mathbf{X}} = \mathbf{X} - \bar{\mathbf{X}}\) of predictors for the observations (shown as points or case labels), together with principal component coefficients for the variables (shown as vectors) in the same 2D (or 3D) space.
However the standard biplot is less useful for visualizing the
relations among the predictors that lead to nearly collinear relations.
Instead, biplots of the smallest dimensions show these
relations directly, and can show other features of the data as well,
such as outliers and leverage points. We use
prcomp(X, scale.=TRUE) to obtain the PCA of the correlation
matrix of the predictors:
cars.X <- cars |>
select(where(is.numeric)) |>
select(-mpg) |>
tidyr::drop_na()
cars.pca <- prcomp(cars.X, scale. = TRUE)
cars.pca
#> Standard deviations (1, .., p=6):
#> [1] 2.070 0.911 0.809 0.367 0.245 0.189
#>
#> Rotation (n x k) = (6 x 6):
#> PC1 PC2 PC3 PC4 PC5 PC6
#> cylinder -0.454 0.1869 -0.168 0.659 -0.2711 0.4725
#> engine -0.467 0.1628 -0.134 0.193 -0.0109 -0.8364
#> horse -0.462 0.0177 0.123 -0.620 -0.6123 0.1067
#> weight -0.444 0.2598 -0.278 -0.350 0.6860 0.2539
#> accel 0.330 0.2098 -0.865 -0.143 -0.2774 -0.0337
#> year 0.237 0.9092 0.335 -0.025 -0.0624 -0.0142The standard deviations above are the square roots \(\sqrt{\lambda_j}\) of the eigenvalues of
the correlation matrix, and are returned in the sdev
component of the "prcomp" object. The eigenvectors are
returned in the rotation component, whose directions are
arbitrary.
# Make labels for dimensions include % of variance
pct <- 100 *(cars.pca$sdev^2) / sum(cars.pca$sdev^2)
lab <- glue::glue("Dimension {1:6} ({round(pct, 2)}%)")
# Direction of eigenvectors is arbitrary. Reflect them
cars.pca$rotation <- -cars.pca$rotationThe collinearity biplot is then constructed as follows:
op <- par(lwd = 2, xpd = NA )
biplot(cars.pca,
choices=6:5, # only the last two dimensions
scale=0.5, # symmetric biplot scaling
cex=c(0.6, 1), # character sizes for points and vectors
col = c("black", "blue"),
expand = 1.7, # expand variable vectors for visibility
xlab = lab[6],
ylab = lab[5],
xlim = c(-0.7, 0.5),
ylim = c(-0.8, 0.5)
)
par(op)
The projections of the variable vectors on the Dimension 5 and Dimension 6 axes are proportional to their variance proportions shown above. The relative lengths of these variable vectors can be considered to indicate the extent to which each variable contributes to collinearity for these two near-singular dimensions.
Thus, we see again that Dimension 6 is largely determined by
engine size, with a substantial (negative) relation to
cylinder. Dimension 5 has its’ strongest relations to
weight and horse.
Moreover, there is one observation, #20, that stands out as an outlier in predictor space, far from the centroid. It turns out that this vehicle, a Buick Estate wagon, is an early-year (1970) American behemoth, with an 8-cylinder, 455 cu. in, 225 horse-power engine, and able to go from 0 to 60 mph in 10 sec. (Its MPG is only slightly under-predicted from the regression model, however.)
Collinearity is often a data problem, for which there is no magic cure. Nevertheless there are some general guidelines and useful techniques to address this problem.
Pure prediction: If we are only interested in predicting / explaining an outcome, and not the model coefficients or which are “significant”, collinearity can be largely ignored. The fitted values are unaffected by collinearity.
structural collinearity: Sometimes collinearity results from structural relations among the variables:
For example, polynomial terms, like \(x, x^2, x^3\) or interaction terms like \(x_1, x_2, x_1 * x_2\) are necessarily correlated. A simple cure is to center the predictors at their means, using \(x - \bar{x}, (x - \bar{x})^2, (x - \bar{x})^3\) or \((x_1 - \bar{x}_1), (x_2 - \bar{x}_2), (x_1 - \bar{x}_1) * (x_2 - \bar{x}_2)\)
When some predictors share a common cause, as in GNP or population in time-series or cross-national data, you can reduce collinearity by re-defining predictors to reflect per capita measures.
Model re-specification:
Drop one or more regressors that have a high VIF if they are not deemed to be essential
Replace highly correlated regressors with linear combination(s) of them. For example, two related variables, \(x_1\) and \(x_2\) can be replaced without any loss of information by replacing them with their sum and difference, \(z_1 = x_1 + x_2\) and \(z_2 = x_1 - x_2\).
Statistical remedies:
Transform the predictors to uncorrelated principal components
use regularization methods such as ridge
regression and lasso, which correct for collinearity by introducing
shrinking coefficients towards 0, introducing a small amount of bias, .
See the genridge package
and its pkgdown
documentation for visualization methods.
use Bayesian regression; if multicollinearity prevents a regression coefficient from being estimated precisely, then a prior on that coefficient will help to reduce its posterior variance.
Belsley, D.A., Kuh, E. and Welsch, R. (1980). Regression Diagnostics, New York: John Wiley & Sons.
Belsley, D.A. (1991). Conditioning diagnostics, collinearity and weak data in regression. New York: John Wiley & Sons.
Friendly, M., & Kwan, E. (2009). “Where’s Waldo: Visualizing Collinearity Diagnostics.” The American Statistician, 63, 56–65. Online: https://www.datavis.ca/papers/viscollin-tast.pdf. Supp. materials: https://www.datavis.ca/papers/viscollin/
Gabriel, K. R. (1971). The Biplot Graphic Display of Matrices with Application to Principal Components Analysis. Biometrics, 58, 453–467.
Gower, J. C., & Hand, D. J. (1996). Biplots. London: Chapman & Hall.
Kwan, E., Lu, I. R. R., & Friendly, M. (2009). Tableplot: A new tool for assessing precise predictions. Zeitschrift Für Psychologie / Journal of Psychology, 217, 38–48.