SGDinference is an R package that provides estimation and inference methods for large-scale mean and quantile regression models via stochastic (sub-)gradient descent (S-subGD) algorithms. The inference procedure handles cross-sectional data sequentially:
The methodology used in the SGDinference package is described in detail in the following papers:
Lee, S., Liao, Y., Seo, M.H. and Shin, Y., 2022. Fast and robust online inference with stochastic gradient descent via random scaling. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 36, No. 7, pp. 7381-7389). https://doi.org/10.1609/aaai.v36i7.20701.
Lee, S., Liao, Y., Seo, M.H. and Shin, Y., 2023. Fast Inference for Quantile Regression with Tens of Millions of Observations. arXiv:2209.14502 [econ.EM] https://doi.org/10.48550/arXiv.2209.14502.
You can install the development version from GitHub with:
# install.packages("devtools") # if you have not installed "devtools" package
devtools::install_github("SGDinference-Lab/SGDinference")We begin by calling the SGDinference package.
To illustrate the usefulness of the package, we use a small dataset included in the package. Specifically, the Census2000 dataset from Acemoglu and Autor (2011) consists of observations on 26,120 nonwhite, female workers. This small dataset is constructed from “microwage2000_ext.dta” at https://economics.mit.edu/people/faculty/david-h-autor/data-archive. Observations are dropped if hourly wages are missing or years of education are smaller than 6. Then, a 5 percent random sample is drawn to make the dataset small. The following three variables are included:
We now define the variables.
As a benchmark, we first estimate the Mincer equation and report the point estimates and their 95% heteroskedasticity-robust confidence intervals.
mincer = lm(y ~ edu + exp + exp2)
inference = lmtest::coefci(mincer, df = Inf,
vcov = sandwich::vcovHC)
results = cbind(mincer$coefficients,inference)
colnames(results)[1] = "estimate"
print(results)
#> estimate 2.5 % 97.5 %
#> (Intercept) 0.58114741 0.52705757 0.63523726
#> edu 0.12710477 0.12329983 0.13090971
#> exp 0.03108721 0.02877637 0.03339806
#> exp2 -0.04498841 -0.05070846 -0.03926835We now estimate the same model using SGD.
mincer_sgd = sgdi_lm(y ~ edu + exp + exp2)
print(mincer_sgd)
#> Call:
#> sgdi_lm(formula = y ~ edu + exp + exp2)
#>
#> Coefficients:
#> Coefficient CI.Lower CI.Upper
#> (Intercept) 0.58714627 0.51899447 0.65529806
#> edu 0.12651235 0.12290359 0.13012112
#> exp 0.03152331 0.02788511 0.03516150
#> exp2 -0.04601193 -0.05566846 -0.03635539
#>
#> Significance Level: 95 %It can be seen that the estimation results are similar between two methods. There is a different command that only computes the estimates but not confidence intervals.
mincer_sgd = sgd_lm(y ~ edu + exp + exp2)
print(mincer_sgd)
#> Call:
#> sgd_lm(formula = y ~ edu + exp + exp2)
#>
#> Coefficients:
#> Coefficient
#> (Intercept) 0.58621823
#> edu 0.12658176
#> exp 0.03152287
#> exp2 -0.04599148We compare the execution times between two versions and find that there is not much difference in this simple example. By construction, it takes more time to conduct inference via sgdi_lm.
library(microbenchmark)
res <- microbenchmark(sgd_lm(y ~ edu + exp + exp2),
sgdi_lm(y ~ edu + exp + exp2),
times=100L)
print(res)
#> Unit: milliseconds
#> expr min lq mean median uq
#> sgd_lm(y ~ edu + exp + exp2) 7.612649 7.783084 8.795013 7.939131 9.419628
#> sgdi_lm(y ~ edu + exp + exp2) 9.605035 9.805727 10.646169 10.028305 10.539734
#> max neval
#> 15.17188 100
#> 14.60316 100To plot the SGD path, we first construct a SGD path for the return to education coefficients.
Then, we can plot the SGD path.
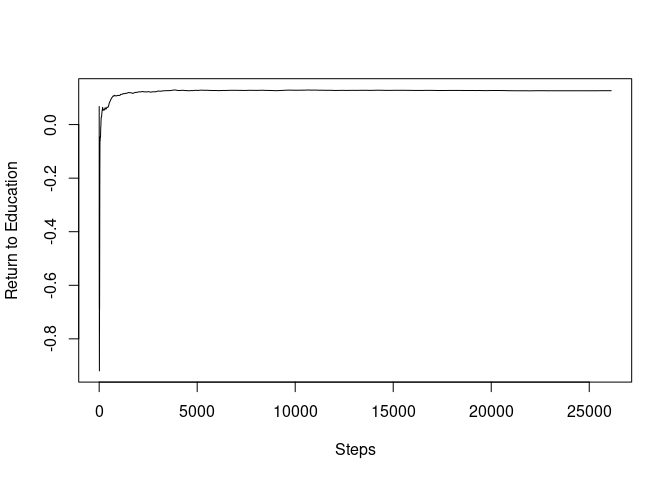
To observe the initial paths, we now truncate the paths up to 2,000.

print(c("2000th step", mincer_sgd_path$path_coefficients[2000]))
#> [1] "2000th step" "0.121832196962998"
print(c("Final Estimate", mincer_sgd_path$coefficients[2]))
#> [1] "Final Estimate" "0.126481851251926"It can be seen that the SGD path almost converged only after the 2,000 steps, less than 10% of the sample size.
See the vignette for the quantile regression example.
Acemoglu, D. and Autor, D., 2011. Skills, tasks and technologies: Implications for employment and earnings. In Handbook of labor economics (Vol. 4, pp. 1043-1171). Elsevier.
Lee, S., Liao, Y., Seo, M.H. and Shin, Y., 2022. Fast and robust online inference with stochastic gradient descent via random scaling. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 36, No. 7, pp. 7381-7389). https://doi.org/10.1609/aaai.v36i7.20701.
Lee, S., Liao, Y., Seo, M.H. and Shin, Y., 2023. Fast Inference for Quantile Regression with Tens of Millions of Observations. arXiv:2209.14502 [econ.EM] https://doi.org/10.48550/arXiv.2209.14502.