 ## The basic disequilibrium model
The basic model is the simplest disequilibrium model of the package as
it basically imposes no assumption on the market structure regarding
price movements (Fair and Jaffee 1972; Maddala and Nelson 1974). In
contrast with the equilibrium model, the market-clearing condition is
replaced by the short-side rule, which stipulates that the minimum
between the demanded and supplied quantities is observed. The
econometrician does not need to specify whether an observation belongs
to the demand or the supply side since the estimation of the model will
allocate the observations on the demand or supply side so that the
likelihood is maximized.
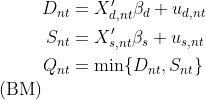
## The basic disequilibrium model
The basic model is the simplest disequilibrium model of the package as
it basically imposes no assumption on the market structure regarding
price movements (Fair and Jaffee 1972; Maddala and Nelson 1974). In
contrast with the equilibrium model, the market-clearing condition is
replaced by the short-side rule, which stipulates that the minimum
between the demanded and supplied quantities is observed. The
econometrician does not need to specify whether an observation belongs
to the demand or the supply side since the estimation of the model will
allocate the observations on the demand or supply side so that the
likelihood is maximized.
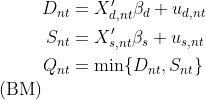
 ## The directional disequilibrium model
The directional model attaches an additional equation to the system of
the basic model. The added equation is a sample separation condition
based on the direction of the price movements (Fair and Jaffee 1972;
Maddala and Nelson 1974). When prices increase at a given date, an
observation is assumed to belong on the supply side. When prices fall,
an observation is assumed to belong on the demand side. In short, this
condition separates the sample before the estimation and uses this
separation as additional information in the estimation procedure.
Although, when appropriate, more information improves estimations, it
also, when inaccurate, intensifies misspecification problems. Therefore,
the additional structure of the directional model does not guarantee
better estimates in comparison with the basic model.
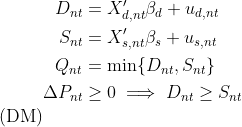
## The directional disequilibrium model
The directional model attaches an additional equation to the system of
the basic model. The added equation is a sample separation condition
based on the direction of the price movements (Fair and Jaffee 1972;
Maddala and Nelson 1974). When prices increase at a given date, an
observation is assumed to belong on the supply side. When prices fall,
an observation is assumed to belong on the demand side. In short, this
condition separates the sample before the estimation and uses this
separation as additional information in the estimation procedure.
Although, when appropriate, more information improves estimations, it
also, when inaccurate, intensifies misspecification problems. Therefore,
the additional structure of the directional model does not guarantee
better estimates in comparison with the basic model.
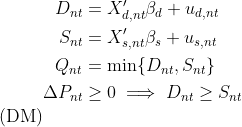
 ## A disequilibrium model with deterministic price dynamics
The separation rule of the directional model classifies observations on
the demand or supply-side based in a binary fashion, which is not always
flexible, as observations that correspond to large shortages/surpluses
are treated the same with observations that correspond to small
shortages/ surpluses. The deterministic adjustment model of the package
replaces this binary separation rule with a quantitative one (Fair and
Jaffee 1972; Maddala and Nelson 1974). The magnitude of the price
movements is analogous to the magnitude of deviations from the
market-clearing condition. This model offers a flexible estimation
alternative, with one extra degree of freedom in the estimation of price
dynamics, that accounts for market forces that are in alignment with
standard economic reasoning. By letting
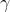 approach zero, the equilibrium model can be obtained as a
limiting case of this model.
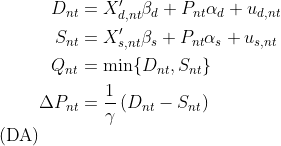
## A disequilibrium model with deterministic price dynamics
The separation rule of the directional model classifies observations on
the demand or supply-side based in a binary fashion, which is not always
flexible, as observations that correspond to large shortages/surpluses
are treated the same with observations that correspond to small
shortages/ surpluses. The deterministic adjustment model of the package
replaces this binary separation rule with a quantitative one (Fair and
Jaffee 1972; Maddala and Nelson 1974). The magnitude of the price
movements is analogous to the magnitude of deviations from the
market-clearing condition. This model offers a flexible estimation
alternative, with one extra degree of freedom in the estimation of price
dynamics, that accounts for market forces that are in alignment with
standard economic reasoning. By letting
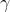 approach zero, the equilibrium model can be obtained as a
limiting case of this model.
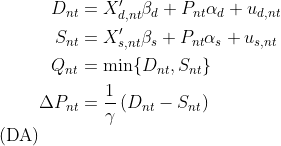
 ## A disequilibrium model with stochastic price dynamics
The last model of the package extends the price dynamics of the
deterministic adjustment model by adding additional explanatory
variables and a stochastic term. The latter term, in particular, makes
the price adjustment mechanism stochastic and, deviating from the
structural assumptions of models
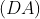 and
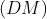, abstains from imposing any separation assumption on the sample
(Maddala and Nelson 1974; Quandt and Ramsey 1978). The estimation of
this model offers the highest degree of freedom, accompanied, however,
by a significant increase in estimation complexity, which can hinder the
stability of the procedure and the numerical accuracy of the outcomes.
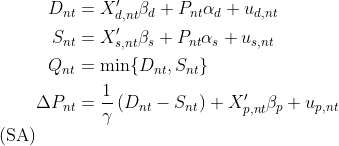
## A disequilibrium model with stochastic price dynamics
The last model of the package extends the price dynamics of the
deterministic adjustment model by adding additional explanatory
variables and a stochastic term. The latter term, in particular, makes
the price adjustment mechanism stochastic and, deviating from the
structural assumptions of models
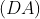 and
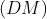, abstains from imposing any separation assumption on the sample
(Maddala and Nelson 1974; Quandt and Ramsey 1978). The estimation of
this model offers the highest degree of freedom, accompanied, however,
by a significant increase in estimation complexity, which can hinder the
stability of the procedure and the numerical accuracy of the outcomes.
 # Installation and documentation
The released version of
[*markets*](https://CRAN.R-project.org/package=markets) can be installed
from [CRAN](https://CRAN.R-project.org) with:
``` r
install.packages("markets")
```
The source code of the in-development version can be downloaded from
[GitHub](https://github.com/pi-kappa-devel/markets).
After installing it, there is a basic-usage example installed with it.
To see it type the command
``` r
vignette('basic_usage')
```
Online documentation is available for both the
[released](https://www.markets.pikappa.eu) and
[in-development](https://www.markets.pikappa.eu/dev/) versions of the
package. The documentation files can also be accessed in `R` by typing
``` r
?? markets
```
An overview of the package’s functionality was presented in the session
Trends, Markets, Models of the
[useR\!2021](https://user2021.r-project.org/) conference. The recording
of the session, including the talk for this package, can be found in the
video that follows. The presentation slides of the talk are also
available [here](https://talks.pikappa.eu/useR!2021/).
# Installation and documentation
The released version of
[*markets*](https://CRAN.R-project.org/package=markets) can be installed
from [CRAN](https://CRAN.R-project.org) with:
``` r
install.packages("markets")
```
The source code of the in-development version can be downloaded from
[GitHub](https://github.com/pi-kappa-devel/markets).
After installing it, there is a basic-usage example installed with it.
To see it type the command
``` r
vignette('basic_usage')
```
Online documentation is available for both the
[released](https://www.markets.pikappa.eu) and
[in-development](https://www.markets.pikappa.eu/dev/) versions of the
package. The documentation files can also be accessed in `R` by typing
``` r
?? markets
```
An overview of the package’s functionality was presented in the session
Trends, Markets, Models of the
[useR\!2021](https://user2021.r-project.org/) conference. The recording
of the session, including the talk for this package, can be found in the
video that follows. The presentation slides of the talk are also
available [here](https://talks.pikappa.eu/useR!2021/).
 # A practical example
This is a basic example that illustrates how a model of the package can
be estimated. The package is loaded in the standard way.
``` r
library(markets)
```
The example uses simulated data. The *markets* package offers a function
to simulate data from data generating processes that correspond to the
models that the package provides.
``` r
model_tbl <- simulate_data(
"diseq_basic", 10000, 5,
-1.9, 36.9, c(2.1, -0.7), c(3.5, 6.25),
2.8, 34.2, c(0.65), c(1.15, 4.2),
NA, NA, c(NA),
seed = 42
)
```
Models are initialized by a constructor. In this example, a basic
disequilibrium model is estimated. There are also other models available
(see [Design and functionality](#design-and-functionality)). The
constructor sets the model’s parameters and performs the necessary
initialization processes. The following variables specify this example’s
parameterization.
- The models can be estimated both with panel and time series data.
The constructor expects both a subject and a time identifier in
order to perform the necessary initialization operations (these are
respectively given by `id` and `date` in the simulated data of this
example). The observation identification of the data is
automatically generated by composing the subject and time
identifiers. The resulting composite key is the combination of
columns that uniquely identify a record of the dataset.
- The observable traded quantity variable (given by `Q` in this
example’s simulated data). The demanded and supplied quantities are
not observable, and they are identified either based on the market
clearing condition or the short side rule.
- The price variable, which is named after `P` in the simulated data.
- The right-hand side specifications of the demand and supply
equations. The expressions are specified similarly to the
expressions of formulas of linear models. Indicator variables and
interactions are created automatically by the constructor.
- The verbosity level controls the level of messaging. The object
displays
- error: always,
- warning: ≥ 1,
- info: ≥ 2,
- verbose: ≥ 3 and
- debug: ≥ 4.
``` r
verbose <- 0
```
- Should the model estimation allow for correlated demand and supply
shocks?
``` r
correlated_shocks <- TRUE
```
The model is estimated with default options by a simple call. See the
documentation of `estimate` for more details and options.
``` r
fit <- diseq_basic(
Q | P | id | date ~ P + Xd1 + Xd2 + X1 + X2 | P + Xs1 + X1 + X2,
model_tbl, correlated_shocks = correlated_shocks, verbose = verbose
)
```
The results can be inspected in the usual fashion via `summary`.
``` r
summary(fit)
```
## Basic Model for Markets in Disequilibrium:
## Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
## Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
## Short Side Rule : Q = min(D_Q, S_Q)
## Shocks : Correlated
## Nobs : 50000
## Sample Separation : Not Separated
## Quantity Var : Q
## Price Var : P
## Key Var(s) : id, date
## Time Var : date
##
## Maximum likelihood estimation:
## Method : BFGS
## Convergence Status : success
## Starting Values :
## D_P D_CONST D_Xd1 D_Xd2 D_X1 D_X2 S_P
## 1.2430 32.8102 0.6986 -0.2362 1.9377 4.8826 1.2390
## S_CONST S_Xs1 S_X1 S_X2 D_VARIANCE S_VARIANCE RHO
## 32.8104 0.4500 1.9376 4.8819 3.8528 4.2008 0.0000
##
## Coefficients:
## Estimate Std. Error z value Pr(z)
## D_P -1.924718 0.013833 -139.1346 0.0000
## D_CONST 36.937193 0.021933 1684.0868 0.0000
## D_Xd1 2.110786 0.009405 224.4360 0.0000
## D_Xd2 -0.691555 0.008147 -84.8864 0.0000
## D_X1 3.521398 0.009738 361.6230 0.0000
## D_X2 6.262825 0.009397 666.4653 0.0000
## S_P 2.797103 0.007373 379.3764 0.0000
## S_CONST 34.188334 0.007529 4540.9220 0.0000
## S_Xs1 0.663960 0.005615 118.2557 0.0000
## S_X1 1.139702 0.006086 187.2806 0.0000
## S_X2 4.203214 0.005976 703.3021 0.0000
## D_VARIANCE 0.996663 0.012529 79.5456 0.0000
## S_VARIANCE 1.006628 0.008312 121.0987 0.0000
## RHO -0.009219 0.026586 -0.3467 0.7288
##
## -2 log L: 138460
# Design and functionality
The equilibrium model can be estimated either using two-stage least
squares or full information maximum likelihood. The two methods are
asymptotically equivalent. The class for which both of these estimation
methods are implemented is
- `equilibrium_model`.
In total, there are four disequilibrium models, which are all estimated
using full information maximum likelihood. By default, the estimations
use analytically calculated gradient expressions, but the user has the
ability to override this behavior. The classes that implement the four
disequilibrium models are
- `diseq_basic`,
- `diseq_directional`,
- `diseq_deterministic_adjustment`, and
- `diseq_stochastic_adjustment`.
The package organizes these classes in a simple object oriented
hierarchy.
# A practical example
This is a basic example that illustrates how a model of the package can
be estimated. The package is loaded in the standard way.
``` r
library(markets)
```
The example uses simulated data. The *markets* package offers a function
to simulate data from data generating processes that correspond to the
models that the package provides.
``` r
model_tbl <- simulate_data(
"diseq_basic", 10000, 5,
-1.9, 36.9, c(2.1, -0.7), c(3.5, 6.25),
2.8, 34.2, c(0.65), c(1.15, 4.2),
NA, NA, c(NA),
seed = 42
)
```
Models are initialized by a constructor. In this example, a basic
disequilibrium model is estimated. There are also other models available
(see [Design and functionality](#design-and-functionality)). The
constructor sets the model’s parameters and performs the necessary
initialization processes. The following variables specify this example’s
parameterization.
- The models can be estimated both with panel and time series data.
The constructor expects both a subject and a time identifier in
order to perform the necessary initialization operations (these are
respectively given by `id` and `date` in the simulated data of this
example). The observation identification of the data is
automatically generated by composing the subject and time
identifiers. The resulting composite key is the combination of
columns that uniquely identify a record of the dataset.
- The observable traded quantity variable (given by `Q` in this
example’s simulated data). The demanded and supplied quantities are
not observable, and they are identified either based on the market
clearing condition or the short side rule.
- The price variable, which is named after `P` in the simulated data.
- The right-hand side specifications of the demand and supply
equations. The expressions are specified similarly to the
expressions of formulas of linear models. Indicator variables and
interactions are created automatically by the constructor.
- The verbosity level controls the level of messaging. The object
displays
- error: always,
- warning: ≥ 1,
- info: ≥ 2,
- verbose: ≥ 3 and
- debug: ≥ 4.
``` r
verbose <- 0
```
- Should the model estimation allow for correlated demand and supply
shocks?
``` r
correlated_shocks <- TRUE
```
The model is estimated with default options by a simple call. See the
documentation of `estimate` for more details and options.
``` r
fit <- diseq_basic(
Q | P | id | date ~ P + Xd1 + Xd2 + X1 + X2 | P + Xs1 + X1 + X2,
model_tbl, correlated_shocks = correlated_shocks, verbose = verbose
)
```
The results can be inspected in the usual fashion via `summary`.
``` r
summary(fit)
```
## Basic Model for Markets in Disequilibrium:
## Demand RHS : D_P + D_Xd1 + D_Xd2 + D_X1 + D_X2
## Supply RHS : S_P + S_Xs1 + S_X1 + S_X2
## Short Side Rule : Q = min(D_Q, S_Q)
## Shocks : Correlated
## Nobs : 50000
## Sample Separation : Not Separated
## Quantity Var : Q
## Price Var : P
## Key Var(s) : id, date
## Time Var : date
##
## Maximum likelihood estimation:
## Method : BFGS
## Convergence Status : success
## Starting Values :
## D_P D_CONST D_Xd1 D_Xd2 D_X1 D_X2 S_P
## 1.2430 32.8102 0.6986 -0.2362 1.9377 4.8826 1.2390
## S_CONST S_Xs1 S_X1 S_X2 D_VARIANCE S_VARIANCE RHO
## 32.8104 0.4500 1.9376 4.8819 3.8528 4.2008 0.0000
##
## Coefficients:
## Estimate Std. Error z value Pr(z)
## D_P -1.924718 0.013833 -139.1346 0.0000
## D_CONST 36.937193 0.021933 1684.0868 0.0000
## D_Xd1 2.110786 0.009405 224.4360 0.0000
## D_Xd2 -0.691555 0.008147 -84.8864 0.0000
## D_X1 3.521398 0.009738 361.6230 0.0000
## D_X2 6.262825 0.009397 666.4653 0.0000
## S_P 2.797103 0.007373 379.3764 0.0000
## S_CONST 34.188334 0.007529 4540.9220 0.0000
## S_Xs1 0.663960 0.005615 118.2557 0.0000
## S_X1 1.139702 0.006086 187.2806 0.0000
## S_X2 4.203214 0.005976 703.3021 0.0000
## D_VARIANCE 0.996663 0.012529 79.5456 0.0000
## S_VARIANCE 1.006628 0.008312 121.0987 0.0000
## RHO -0.009219 0.026586 -0.3467 0.7288
##
## -2 log L: 138460
# Design and functionality
The equilibrium model can be estimated either using two-stage least
squares or full information maximum likelihood. The two methods are
asymptotically equivalent. The class for which both of these estimation
methods are implemented is
- `equilibrium_model`.
In total, there are four disequilibrium models, which are all estimated
using full information maximum likelihood. By default, the estimations
use analytically calculated gradient expressions, but the user has the
ability to override this behavior. The classes that implement the four
disequilibrium models are
- `diseq_basic`,
- `diseq_directional`,
- `diseq_deterministic_adjustment`, and
- `diseq_stochastic_adjustment`.
The package organizes these classes in a simple object oriented
hierarchy.
 Concerning post estimation analysis, the package offers functionality to
calculate
- shortage probabilities,
- marginal effects on shortage probabilities,
- point estimates of normalized shortages,
- point estimates of relative shortages,
- aggregate demand and supply,
- post-estimation classification of observations in demand and supply,
- heteroscedasticity-adjusted (Huber-White) standard errors, and
- clustered standard errors.
# Alternative packages
The estimation of the basic model is also supported by the package
[*Disequilibrium*](https://CRAN.R-project.org/package=Disequilibrium).
By default, the *Disequilibrium* package numerically approximates the
gradient when optimizing the likelihood. In contrast, *markets* uses
analytically calculated expressions for the likelihood, which can reduce
the duration of estimating the model. In addition, it allows the user to
override this behavior and use the numerically approximated gradient.
There is no alternative package that supports the out-of-the-box
estimation of the other three disequilibrium models of *markets*.
# Planned extensions
The package is planned to be expanded in the following ways:
1. The package should become more inclusive by adding additional market
models.
2. Single-command functionality for the market-clearing tests
(e.g. (Karapanagiotis, n.d.; Hwang 1980; Quandt 1978)) should be
included in the package.
3. Alternative estimation methods (e.g. (Zilinskas and Bogle 2006;
Quandt and Ramsey 1978)) could also be implemented.
# Contributors
[Pantelis Karapanagiotis](https://www.pikappa.eu)
Feel free to join, share, contribute, distribute.
# License
The code is distributed under the MIT License.
# References
Concerning post estimation analysis, the package offers functionality to
calculate
- shortage probabilities,
- marginal effects on shortage probabilities,
- point estimates of normalized shortages,
- point estimates of relative shortages,
- aggregate demand and supply,
- post-estimation classification of observations in demand and supply,
- heteroscedasticity-adjusted (Huber-White) standard errors, and
- clustered standard errors.
# Alternative packages
The estimation of the basic model is also supported by the package
[*Disequilibrium*](https://CRAN.R-project.org/package=Disequilibrium).
By default, the *Disequilibrium* package numerically approximates the
gradient when optimizing the likelihood. In contrast, *markets* uses
analytically calculated expressions for the likelihood, which can reduce
the duration of estimating the model. In addition, it allows the user to
override this behavior and use the numerically approximated gradient.
There is no alternative package that supports the out-of-the-box
estimation of the other three disequilibrium models of *markets*.
# Planned extensions
The package is planned to be expanded in the following ways:
1. The package should become more inclusive by adding additional market
models.
2. Single-command functionality for the market-clearing tests
(e.g. (Karapanagiotis, n.d.; Hwang 1980; Quandt 1978)) should be
included in the package.
3. Alternative estimation methods (e.g. (Zilinskas and Bogle 2006;
Quandt and Ramsey 1978)) could also be implemented.
# Contributors
[Pantelis Karapanagiotis](https://www.pikappa.eu)
Feel free to join, share, contribute, distribute.
# License
The code is distributed under the MIT License.
# References