This package provides functions to evaluate moments of ratios (and products) of quadratic forms in normal variables, specifically using recursive algorithms developed by Bao and Kan (2013) and Hillier et al. (2014). Generating functions for these moments are closely related to the top-order zonal and invariant polynomials of matrix arguments. It also provides some functions to evaluate distribution and density functions of simple ratios of quadratic forms in normal variables using several methods from Imhof (1961), Hillier (2001), Forchini (2002, 2005), Butler and Paolella (2008), and Broda and Paolella (2009).
There exist a couple of Matlab programs developed by
Raymond Kan (available from https://www-2.rotman.utoronto.ca/~kan/) for evaluating
the moments, but this R package is an independent project
(not a fork or translation) and has different functionalities, including
evaluation of moments of multiple ratios of a particular form and
scaling to avoid numerical overflow. This has originally been developed
for a biological application, specifically for evaluating average
evolvability measures in evolutionary quantitative genetics (Watanabe, 2023), but can be used for a
broader class of statistics.
WARNING Installation size of this package
can be very large (>100 MB on Linux and macOS; ~3 MB on Windows with
a recent version (>= 4.2) of Rtools), as it
involves lots of RcppEigen functions.
install.packages("qfratio")## Install devtools first:
# install.packages("devtools")
## Recommended installation (pandoc required):
devtools::install_github("watanabe-j/qfratio", dependencies = TRUE, build_vignettes = TRUE)
## Minimal installation:
# devtools::install_github("watanabe-j/qfratio")Imports: Rcpp, MASS
LinkingTo: Rcpp, RcppEigen
Suggests: gsl, mvtnorm, CompQuadForm, graphics, stats, testthat (>= 3.0.0),
rlang (>= 0.4.7), knitr, rmarkdownIf installing from source, you also need pandoc for correctly building
the vignette. For pandoc < 2.11,
pandoc-citeproc is required as well. (Never mind if you use
RStudio, which appears to have them bundled.)
This package has two major functionalities: evaluating moments and distribution function of ratios of quadratic forms in normal variables.
This functionality concerns evaluation of the following moments: \(\mathrm{E} \left( \left( \mathbf{x}^T \mathbf{A} \mathbf{x} \right)^p / \left( \mathbf{x}^T \mathbf{B} \mathbf{x} \right)^q \right)\) and \(\mathrm{E} \left( \left( \mathbf{x}^T \mathbf{A} \mathbf{x} \right)^p / \left( \mathbf{x}^T \mathbf{B} \mathbf{x} \right)^q \left( \mathbf{x}^T \mathbf{D} \mathbf{x} \right)^r \right)\), where \(\mathbf{x} \sim N_n \left(\boldsymbol{\mu}, \boldsymbol{\Sigma}\right)\).
These quantities are evaluated by qfrm(A, B, p, q, ...)
and qfmrm(A, B, D, p, q, r, ...). Because they are
evaluated as partial sums of infinite series (Smith, 1989, 1993; Hillier
et al., 2009, 2014; Bao and Kan, 2013), the evaluation results
come with an error bound (where available), and a plot
method is defined for inspecting numerical convergence.
## Simple matrices
nv <- 4
A <- diag(1:nv)
B <- diag(sqrt(nv:1))
## Expectation of (x^T A x)^2 / (x^T x)^2 where x ~ N(0, I)
qfrm(A, p = 2)
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 6.666667
#> This value is exact
## Compare with Monte Carlo mean
mean(rqfr(1000, A = A, p = 2))
#> [1] 6.641507
## Expectation of (x^T A x)^1/2 / (x^T x)^1/2
(mom_A0.5 <- qfrm(A, p = 1/2))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 1.567224, Error = -6.335806e-19 (one-sided)
#> Possible range:
#> 1.56722381 1.56722381
## Monte Carlo mean
mean(rqfr(1000, A = A, p = 1/2))
#> [1] 1.569643
plot(mom_A0.5)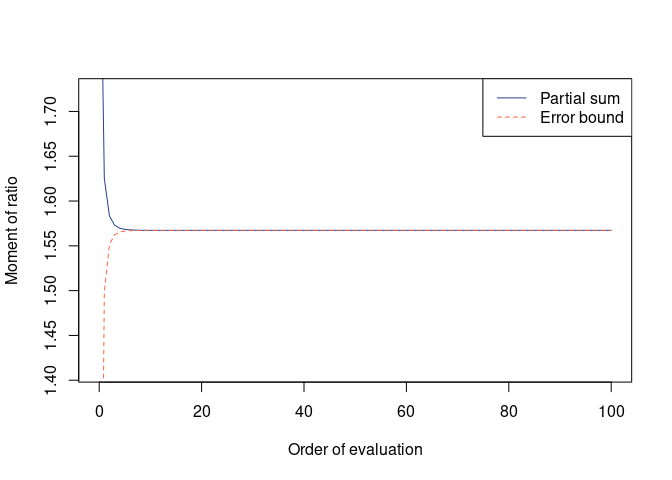
## Expectation of (x^T x) / (x^T A^-1 x)
## = "average conditional evolvability"
(avr_cevoA <- qfrm(diag(nv), solve(A)))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 2.11678, Error = 2.768619e-15 (one-sided)
#> Possible range:
#> 2.11677962 2.11677962
mean(rqfr(1000, A = diag(nv), B = solve(A), p = 1))
#> [1] 2.071851
plot(avr_cevoA)
## Expectation of (x^T x)^2 / (x^T A x) (x^T A^-1 x)
## = "average autonomy"
(avr_autoA <- qfmrm(diag(nv), A, solve(A), p = 2, q = 1, r = 1))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 0.8416553
#> Error bound unavailable; recommended to inspect plot() of this object
mean(rqfmr(1000, A = diag(nv), B = A, D = solve(A), p = 2, q = 1, r = 1))
#> [1] 0.8377911
plot(avr_autoA)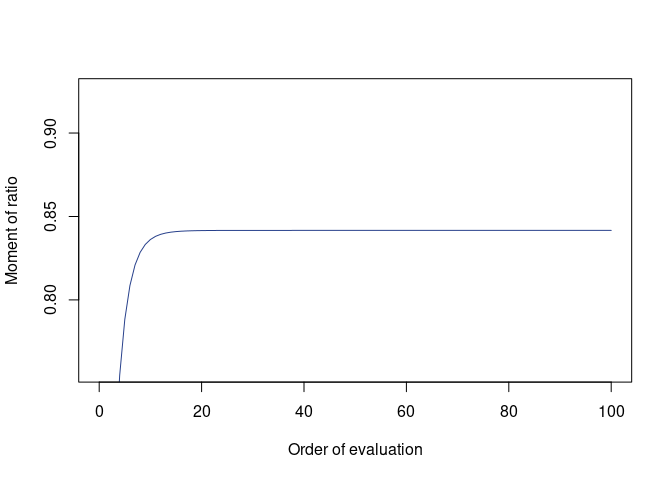
## Expectation of (x^T A B x) / ((x^T A^2 x) (x^T B^2 x))^1/2
## = "average response correlation"
## whose Monte Carlo evaluation is called the "random skewers" analysis,
## while this is essentially an analytic solution (with slight truncation error)
(avr_rcorA <- qfmrm(crossprod(A, B), crossprod(A), crossprod(B),
p = 1, q = 1/2, r = 1/2))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 0.8462192
#> Error bound unavailable; recommended to inspect plot() of this object
mean(rqfmr(1000, A = crossprod(A, B), B = crossprod(A), D = crossprod(B),
p = 1, q = 1/2, r = 1/2))
#> [1] 0.8467811
plot(avr_rcorA)
## More complex (but arbitrary) example
## Expectation of (x^T A x)^2 / (x^T B x)^3 where x ~ N(mu, Sigma)
mu <- 1:nv / nv
Sigma <- diag(runif(nv) * 3)
(mom_A2B3 <- qfrm(A, B, p = 2, q = 3, mu = mu, Sigma = Sigma,
m = 500, use_cpp = TRUE))
#>
#> Moment of ratio of quadratic forms
#>
#> Moment = 0.510947, Error = 0 (two-sided)
#> Possible range:
#> 0.510946975 0.510946975
plot(mom_A2B3)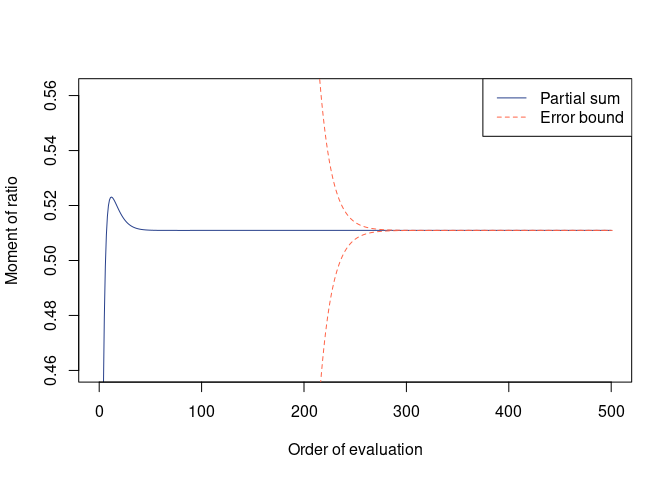
This functionality concerns evaluation of the (cumulative) distribution function and probability density of \(\left( \mathbf{x}^T \mathbf{A} \mathbf{x} / \mathbf{x}^T \mathbf{B} \mathbf{x} \right) ^ p\), where \(\mathbf{x} \sim N_n \left(\boldsymbol{\mu}, \boldsymbol{\Sigma}\right)\).
These are handled by pqfr(quantile, A, B, p, ...) and
dqfr(quantile, A, B, p, ...), whose usage mimics that of
regular distribution-related functions.
## Example parameters
nv <- 4
A <- diag(1:nv)
B <- diag(sqrt(nv:1))
mu <- 1:nv * 0.2
quantiles <- 0:nv + 0.5
## Distribution function and density of
## (x^T A x) / (x^T B x) where x ~ N(0, I)
pqfr(quantiles, A, B)
#> [1] 0.0000000 0.4349385 0.8570354 0.9816503 1.0000000
dqfr(quantiles, A, B)
#> [1] 0.00000000 0.57079928 0.21551262 0.06123152 0.00000000
## Comparing profiles
qseq <- seq.int(1 / sqrt(nv) - 0.2, nv + 0.2, length.out = 100)
## Generate p-value sequences for
## (x^T A x) / (x^T B x) where x ~ N(0, I) vs
## (x^T A x) / (x^T B x) where x ~ N(mu, I)
pseq_central <- pqfr(qseq, A, B)
pseq_noncent <- pqfr(qseq, A, B, mu = mu)
## Graphical comparison
plot(qseq, type = "n", xlim = c(1 / sqrt(nv), nv), ylim = c(0, 1),
xlab = "q", ylab = "F(q)")
lines(qseq, pseq_central, col = "royalblue4", lty = 1)
lines(qseq, pseq_noncent, col = "tomato", lty = 2)
legend("topleft", legend = c("central", "noncentral"),
col = c("royalblue4", "tomato"), lty = 1:2)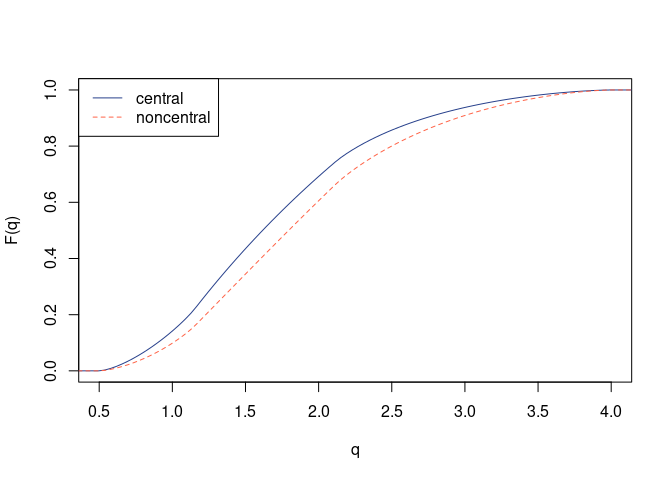
## Generate density sequences for
## (x^T A x) / (x^T B x) where x ~ N(0, I) vs
## (x^T A x) / (x^T B x) where x ~ N(mu, I)
dseq_central <- dqfr(qseq, A, B)
dseq_noncent <- dqfr(qseq, A, B, mu = mu)
## Graphical comparison
plot(qseq, type = "n", xlim = c(1 / sqrt(nv), nv), ylim = c(0, 0.7),
xlab = "q", ylab = "f(q)")
lines(qseq, dseq_central, col = "royalblue4", lty = 1)
lines(qseq, dseq_noncent, col = "tomato", lty = 2)
legend("topright", legend = c("central", "noncentral"),
col = c("royalblue4", "tomato"), lty = 1:2)
This package bundles selected C codes and part of
config.ac from the GNU Scientific Library,
whose copyright belongs to the original authors. See
DESCRIPTION and individual code files in
src/gsl for details. The redistribution complies with the
GNU General Public License version 3.